このページでは、掛け算と割り算が混ざった連続計算の仕方を紹介します。
ここで、前回までのポイントを簡単にまとめたいと思います。具体的な内容は、以前のページをご覧下さい。
掛け算、割り算にはそれぞれC尺を使う方法と、CI尺を使う方法があります。それら4つは連続計算の基本となります。まだはっきりしない人は、ここをご覧下さい。
計算尺で掛け算の連続計算をするときは、「CI尺→C尺→CI尺→C尺→…」と順番に操作していくと楽になるのでした。同様に、割り算のときは「C尺→CI尺→C尺→CI尺→…」と順番に操作していくと楽になるのでした。スタートの計算方法が違うのは、掛け算の場合はCI尺を使ったほうが、割り算の場合はC尺を使ったほうが楽だったからです。できるだけ楽をして計算をしたいのです。
計算尺で計算をするとき(電卓や筆算のときでも同様ですが)、私たちが必要としているのは最終的な答えだけです。途中結果が何であろうが、私たちには関係ないのです。だから、たとえば、1.56×5.26×4.5のとき、1.56×5.26の答えは読み取る必要がありません。むしろ、読み取ろうとしないで下さい。時間の無駄です。ただ、そこに答えがあるということを感じていればいいのです。
CI尺を使って掛け算をした後、C尺を使って連続計算をする場合ですが、このとき一度カーソルをCI尺の1(あるいはCI尺の10)にあわせていると、それは無駄な動作です。なぜなら、カーソル線をCI尺の1(あるいはCI尺の10)にあわせた後、すぐにカーソルをC尺の別のメモリに移動させるからです。そのときは、CI尺を使って掛け算をした後、CI尺の1(あるいはCI尺の10)の下にその答えを感じながら、カーソル線を直接次のC尺のメモリに動かし、計算を続けてください。
C尺を使って割り算をした後、CI尺を使って連続計算をする場合ですが、このとき一度カーソルをC尺の1(あるいはC尺の10)にあわせていると、それは無駄な動作です。なぜなら、カーソル線をC尺の1(あるいはC尺の10)にあわせた後、すぐにカーソルをCI尺の別のメモリに移動させるからです。そのときは、C尺を使って掛け算をした後、C尺の1(あるいはC尺の10)の下にその答えを感じながら、カーソル線を直接次のCI尺のメモリに動かし、計算を続けてください。
いつカーソルを動かして、いつカーソルを動かさないかは、はじめのうちは悩むと思います。しかし、計算尺を使っているうちにだんだん分かってくると思います。
正直に言うと、上のことが分かっていれば新たに覚えることはありません。計算尺を使って、計算しているうちにコツがつかめると思います。
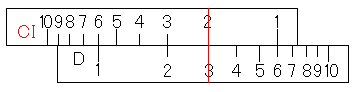
掛け算と割り算の混合計算は、それを順番にやれば答えが出ます。具体例で計算を見てみましょう。「3×2÷4」です。

これで、「3×2」はできましたよね。そして、カーソルをCI尺の4に移します。
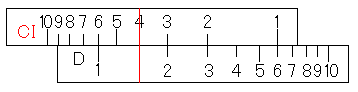
すると、D尺に答えの1.5がありますよね。「あれ?それだけ?」そうなんですね。じっくりと計算方法を眺めてください。今までやってきたことをフル動員すると、計算の原理が分かりますよね。分からないという方は、こちらをご覧下さい。
それでは、割り算が先の場合もやってみましょう。「3÷2×4」です。
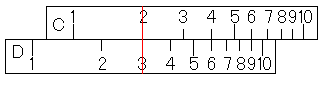
そして、カーソルをC尺の4に合わせます。
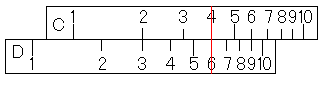
すると、D尺に答えの6がありますよね。じっくりと計算方法を眺めてください。今までやってきたことをフル動員すると、計算の原理が分かりますよね。分からない方は、こちらをご覧下さい。
では、「3×2÷4×6」をやってみましょう。実は、「3×2÷4」の部分は、1.具体的な例1で紹介した方法で計算できます。
そして、あとは「×6」ですね。ここで今の計算尺の状態をもう一度ご覧下さい。

いまは、「D尺に今までの計算の答えがあり、その値にカーソル線が合っていて、そのカーソル線にC尺あるいはCI尺上の前に掛けた(あるいは割った)数字があっている」場合ですね。かぎカッコは前の文章を引用したことを意味しています。掛け算にはC尺を使った方法と、CI尺を使った方法の2つがありました。どちらを使うべきでしょうか?そろそろ計算尺の勘が働くようになってきましたか?今回は、CI尺を使いましょう。
「×6」をするのですから、滑尺を動かして、CI尺の6をカーソル線に合わせます。
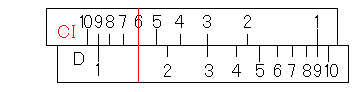
そして、カーソルを動かして、カーソル線をCI尺の1に合わせます。
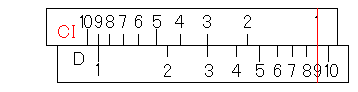
これで、「3×2÷4×6=9」が求まりました。
最後に、「3×2÷4÷5」をやってみましょう。実は、「3×2÷4」の部分は、1.具体的な例1で紹介した方法で計算できます。
そして、あとは「÷5」ですね。ここで今の計算尺の状態をもう一度ご覧下さい。

いまは、D尺に今までの計算の答えがあり、その値にカーソル線が合っていて、そのカーソル線にC尺あるいはCI尺上の前に割った(あるいは掛けた)数字があっている」場合ですね。先ほどと同じで、かぎカッコは前の文章を引用したことを意味しています。割り算にもC尺を使った方法と、CI尺を使った方法の2つがありました。どちらを使うべきでしょうか?もう計算尺の勘が働くようになってきましたね。今回は、C尺を使いましょう。
滑尺を動かして、C尺の5をカーソル線に合わせます。
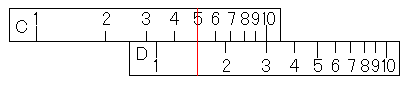
そして、カーソル線をC尺の10に持っていくと、D尺には3、位取りを考えて、「3×2÷4÷5=0.3」です。
もっと増えたら、どうしましょうか?もっと増えても計算の方法は変わりません。掛け算、割り算にはそれぞれC尺を使う方法と、CI尺を使う方法がありますので、どちらが便利かを考えて、計算を続けます。