このページでは、連続計算の仕方を紹介します。掛け算・割り算のまとめで紹介したことを前提として話を進めていきますので、まだお読みになっていない方は、こちらをご覧下さい。
皆さんはすでに掛け算の仕方をご存知です。ということは、掛け算を何回か繰り返すことによって答えを求めることができます。
では、具体的に、2×3×5の計算をして見ましょう。
掛け算が2回出てきますから、これを2つの掛け算に分けて計算します。つまり、まず、2×3をして、その答え6を出します。そして、その6に5をかけます。
ここでは、一番最初に紹介したC尺とD尺を使った方法を紹介します。
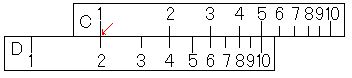
まず、2×3です。では、やってみましょう。C尺の1をD尺の2に合わせます。

次に、カーソル線をC尺の3に合わせます。
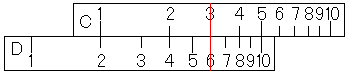
そうすると、D尺に答えの6が出ています。実は、掛け算(1)で紹介した計算とまったく同じでした。
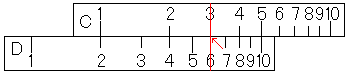
6が求まった後、カーソル線を動かさないで下さい。
今、私たちは「2×3×5」のうち、「2×3」までやりました。後は、この値6に5をかけるだけです。
今、D尺の6にカーソル線が合っていますので、このカーソル線にC尺の10を合わせてください。
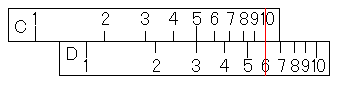
このとき、どうしてC尺の1ではなくてC尺の10を合わせるのでしょうか?そうです。目はずれを避けるためですね。もしC尺の1をあわせていたら、後で困ることになります。どうなるかは皆さんが一度試してみてください。
そして、カーソルを動かして、C尺の5に合わせて下さい。
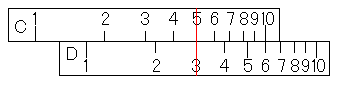
すると、D尺に3があります。計算尺は有効数字の部分だけ計算するのでしたから、3を30だと思えば、答えが求まっています。
ここで、いくつか見ていただきたいことがあります。
2×3のところまではいいと思います。その時にはD尺の6のところにカーソル線があり、そこにC尺の10を合わせました。このとき、私たちは2つの動作をしているのです。すなわち、「2×3の答えを求め(カーソル線の移動)」、「その答えに5をかけるための準備(滑尺の移動)」をしています。C尺とD尺を使った掛け算ではまず掛けられる数をD尺におきました。この動作を省略できるのです。C尺を使った掛け算の仕方をもう一度書いておきます。
もうひとつ、実は、このとき、2×3の答えの6を読む必要がないのです。カーソル線をC尺の3に合わせて、そのカーソル線にC尺の10をセットすれば、2番目の掛け算「(2×3の答え)×5」の準備ができています。
以上のことを確認していただくために、1.25×3.3×8をやってみてください。1.25×3.3は汚い数字になりますが、最終的な答えはきれいな数字になると思います。(答え:33)
上で紹介した方法を使えば、どんな掛け算でもできます。しかし、何度も滑尺やカーソルを動かさなければならず、長い計算では大変不便です。そこで、ちょっと楽できる計算方法を紹介します。
それは、C尺とD尺だけではなく、CI尺も使う方法です。前までのページで、C尺を使った掛け算と、CI尺を使った掛け算の2種類紹介しました。「どうして同じ掛け算をするのに2種類もあるのか?」と疑問に思った方がいらっしゃるかもしれません。それは、連続計算で使うためだったのです。
では、具体的に計算をしてみましょう。ここでは先ほどと同じ2×3×5をしてみたいと思います。ここでも、先に2×3をするのは同じです。
まず、2×3です。では、やってみましょう。C尺の1をD尺の2に合わせます。

次に、カーソル線をC尺の3に合わせます。

そうすると、D尺に答えの6が出ています。

6が求まった後、カーソル線を動かさないで下さいね。
今、私たちは「2×3×5」のうち、「2×3」までやりました。後は、この値6に5をかけるだけです。
ここで、先ほどはC尺の10を合わせましたが、今度はCI尺を使って計算したいのです。CI尺を遣った計算の方法を覚えていますか?
このうち、「D尺の掛けられる数にカーソル線を合わせる」というのはすでにできていますよね。なので、CI尺に5をあわせるところから続けます。
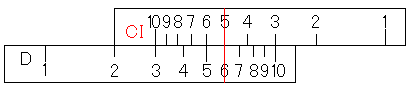
そして、CI尺の10にカーソル線を合わせます。
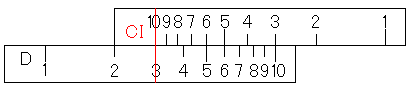
そうすると、D尺に3、つまり、30が求まっています。
以上、掛け算の連続計算の方法を2種類紹介しました。どちらが簡単だったでしょうか?手順は2.のほうが複雑なので、2.は面倒くさいと思ったかもしれません。しかし、計算の手続きとしては2.の方が少ないのです。今のところは3つの数の掛け算までしか紹介していませんが、次の項目で紹介する4個、5個の数字の掛け算になるとその差は顕著になります。2.の方法での連続計算の計算方法を練習してみてください。
1個ずつ計算していく、1.の方法はお分かりいただけると思いますので、C尺とCI尺の両方を用いた2.の計算方法を紹介します。
例によって簡単な式で説明します。前の計算式にちょっとだけ数を足してみました。「2×3×5×2」です。2×3×5の部分は2.で紹介した方法で計算します。念のため、もう一度記しておきます。
まず、2×3です。では、やってみましょう。C尺の1をD尺の2に合わせます。

次に、カーソル線をC尺の3に合わせます。

そうすると、D尺に答えの6が出ています。

CI尺の5をカーソル線にあわせます。

そして、CI尺の10にカーソル線を合わせます。

そうすると、D尺に3、つまり、30が求まっています。
ここからが新しいことです。今の計算尺の状態をじっと眺めてください。私たちはあと、1つの数字を掛けなければなりません。そのかける対象(30の3)はD尺にいます。また、滑尺はその数字(30の3)に合っています。
この後、どうやって2を掛けましょうか?掛け算の方法は2種類知っています。そのうちどちらが楽でしょうか?この場合、C尺を使う方法はまずC尺の1か10をD尺の3にあわせます。それに対して、CI尺を使う方法ではC尺の2をD尺の3にあわせなければなりません。それならば、C尺を使ったほうが楽ですよね。なぜなら、C尺の1はすでにD尺の3に合っていますから。あと私たちがしなければならないのは、カーソル線をC尺の2に移動して、そのD尺のメモリを読むことです。
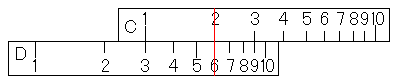
すると、2×3×5×2=60を求めることができたのです。
今まで、いくつかC尺とCI尺を使った連続計算をしてきましたが、ある程度ポイントをつかむことができていると思います。私たちが第一に考えることは、「楽をすること」。このあと、C尺を使ったほうが楽か、それともCI尺を使ったほうが楽なのか、それを考えれば、一番楽な方法で計算を進めることができます。
幸い、連続計算には一定のルールがあります。それは「逆・逆・逆…」です。つまり、「C尺を使ったら今度はCI尺、その次はC尺、そのまた次はCI尺、そのまたまた先はC尺…」ということです。そうすると、無駄なく計算することができます。
今回は「2×3×5×2」の「2×3」の計算をC尺を使いましたが、CI尺を使って計算を始めても構いません。むしろ、掛け算はCI尺を使ったほうが楽ですから、CI尺からはじめることが多いようです。
これは、次の次で説明する、掛け算と割り算が混ざった連続計算のときにとても役立つのですが、次のようなルールがあります。
それから、CI尺を使って掛け算をした後、C尺を使って連続計算をする場合ですが、このとき一度カーソルをCI尺の1(あるいはCI尺の10)にあわせていると、それは無駄な動作です。なぜなら、カーソル線をCI尺の1(あるいはCI尺の10)にあわせた後、すぐにカーソルをC尺の別のメモリに移動させるからです。そのときは、CI尺を使って掛け算をした後、CI尺の1(あるいはCI尺の10)の下にその答えを感じながら、カーソル線を直接次のC尺のメモリに動かし、計算を続けてください。