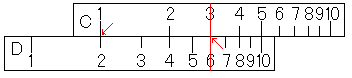
これまでの3ページで、計算尺の基本となる掛け算・割り算の仕方は終わりです。ここで、簡単にまとめておきたいと思います。
「2×3」の仕方です。

「8÷4」の仕方です。
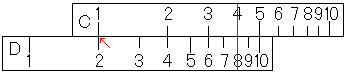
「3×2」の仕方です。
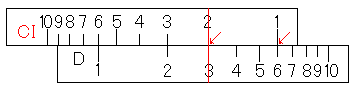
「6÷3」の仕方です。
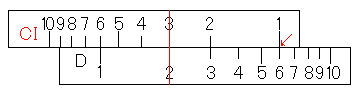
上に、4つの計算方法をまとめてみましたが、見比べてみると結構似ていると思います。では分析してみましょう。
C尺を使った掛け算とCI尺を使った割り算、C尺を使った割り算とCI尺を使った掛け算が似ていると思います。C尺を使った割り算とCI尺を使った掛け算では、計算する2つの数字をカーソル線を介して上下に並べます。それに対して、C尺を使った掛け算とCI尺を使った割り算では、計算する2つの数字が上下に並ぶことなく、滑尺の右端か左端を介して計算します。
上のまとめを見て分かると思いますが、C尺の1とC尺の10は区別せずに使ってかまいません。「C尺の1を使いたかったけど、使えない」というときは、C尺の10を使うことができます。その逆も同様です。また、「CI尺の1を使いたかったけど、使えない」というときは、CI尺の10を使うことができます。その逆も同様です。
「固定尺のD尺の2に滑尺のC尺の3を合わせる」といった、固定尺と滑尺との間で操作する場合には、基本的にカーソル線を使います。つまり、「まずD尺の2にカーソル線を合わせ、カーソル線にC尺の3を合わせる」というようにします。
D尺とCI尺の数字を合わせるなど、離れた数字を合わせるときに使うのは当たり前ですが、このようにC尺とD尺の数字を合わせるときにも使います。
ひとつ実験をしてみましょう。カーソル線を使わないでD尺の1.12とC尺の1.92を合わせてみてください。いずれも目盛りの線は付いていますが、合わせるのはかなり大変だと思います。
ではカーソル線を用いてD尺の1.12とC尺の1.92を合わせるとどうでしょうか。比較的簡単に合わせることができると思います。
カーソル線を使うことによって、メモリを合わせる操作が楽になり、操作ミスも少なくなります。
しかし、カーソル線を使わなくてもいいときがあります。それは滑尺でC尺の1・C尺の10・CI尺の1・CI尺の10を使うときなどです。「固定尺のD尺の2に滑尺のC尺の1を合わせる」ときには、直接「D尺の2にC尺の1をあわせる」ことでかまいません。
これも実験してみましょう。カーソル線を使わずに、D尺の1.12とCI尺の1(C尺の10と同じ)を合わせてみてください。難なく合わせることができると思います。
掛け算、割り算にはそれぞれC尺を使う方法と、CI尺を使う方法があります。どうして2通りもあるのでしょうか?それは、連続計算をするときに役立つからです。しかし、連続的に計算しない場合、つまり2つの数字を掛け合わせるときなどは、好ましい方が決まっています。
掛け算のときはCI尺を使う。割り算のときはC尺を使う。
こういうことです。どうしてかというと、楽だからです。まず、目外れが起きません。これは、とても大切な長所です。「計算したのにメモリが読めなかった」なんて悲しいですよね。それと、連続計算をするようになると分かりますが、こうした方法のほうが連続計算するときに次の手順に移りやすいのです。普段からこちらで慣れていれば、連続計算のときも素直に計算できます。そういう理由で、「掛け算のときはCI尺を使う。割り算のときはC尺を使う。」に慣れていたほうが好ましいです。