さて、いよいよ計算尺の具体的な使い方になるのですが、お手元に何らかの計算尺がありますか?計算尺推進委員会の文章は、ぜひ、実際に計算尺を動かしながらご覧ください。ここに、計算尺の入手方法が書かれていますので、計算尺をお手元に準備してください。
次の項目から、計算尺の簡単な図を用いて説明していきます。おそらく、見た感じで分かると思います。赤の矢印や縦線が注意するところです。赤の縦線はカーソル線を表しています。
それでは早速計算をしてみましょう。
皆さんが小学2年生のとき「にいちがに、ににんがし、にさんがろく、…」と九九を覚えましたよね。この「にさんがろく」を検証してみたいと思います。
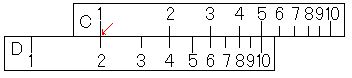
まず、D尺の2に、C尺の1をあわせます。このとき、「滑尺を固定して、固定尺を動かす」のではなくて「滑尺を動かして」あわせます。

次に、カーソルを動かして、カーソル線をC尺の3にあわせます。くれぐれも、このとき滑尺を動かさないようにしてください。
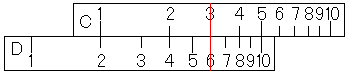
そして、カーソル線のあるD尺のメモリを読みます。
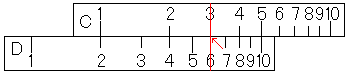
どうですか?ちゃんと6になっていますよね。これで私たちは「にさんがろく」というのは正しかったと分かったのです。
では、「4×2」をやってみてください。上の説明を見ながらで結構です。当然「8」になりましたよね。
それでは、少しだけ数式を出しますので、計算尺で計算してみてください。
計算尺は値を近似値で出します。なので正確な値を求めることはできません。しかし、正確な値にたいした意味がないことは以前説明しました。
「計算の原理なんか分からなくてもいい」という方や、「数学嫌い」という人は、この項目を読み飛ばしてもかまいません。読みたくなったら読んでください。
皆さんは「対数」をご存知ですか?高校数学で登場するlogやlnです。計算尺推進委員会ではlogとlnを使い分けたいと思います。logといえば、底が10の対数、つまりlog10を指すものとします。lnといえば、底がeの対数、つまりlogeを指すものとします。ここでeは自然対数の底(ネイピア数)で、e=2.718281828…です。底が10やeでない対数はそのつど示します。たとえば、log13や、log4.5です。
では、計算尺と定規を準備してください。そして、滑尺を抜き取ってください。そんなことしてもいいのかと心配になるかもしれませんが大丈夫です。取り出したら、定規を使ってC尺の1とC尺の10の間の長さ、C尺の1とC尺の2の間の長さ、C尺の1とC尺の3の間の長さをそれぞれ測ってください。メモリの10分の1まで、つまりたいていは0.01cmまで目分量で読んでください。ちなみに、私の計算尺では次のようになりました。
次に、C尺の1とC尺の10の間の長さに対する、 C尺の1とC尺の2の間の長さと、 C尺の1とC尺の3の間の長さの比を求めてください。つまり、(2)÷(1)と、(3)÷(1)をしてください。ちなみに、私の場合、次の通りです。
いかがでしょうか?x=2のときf(x)=0.3010、x=3のときf(x)=0.4772です。どこかでみた記憶がありませんか?そうです。f(x)=log(x)なんです。これが計算尺のすべての根底にある原理です。メモリをlogで振ってあるのです。ここに、logの表をあげますから、ほかの値でも確かめてみてください。
| x | log(x) |
|---|---|
| 1 | 0.0000 |
| 2 | 0.3010 |
| 3 | 0.4771 |
| 4 | 0.6020 |
| 5 | 0.6990 |
| 6 | 0.7782 |
| 7 | 0.8451 |
| 8 | 0.9031 |
| 9 | 0.9542 |
| 10 | 1.0000 |
では、計算尺で掛け算ができる原理を見てみましょう。
先ほどの2×3で見てみましょう。
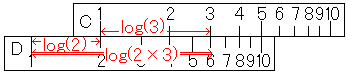
この図でお分かりいただけるでしょうか。log(xy)=log(x)+log(y)という関係式がありましたよね。つまり、C尺で長さlog(2)、D尺で長さlog(3)を準備しておけば、D尺の1からC尺の3の位置までの長さはlog(2)+log(3)=log(2×3)になっているのです。
これで掛け算ができるようになりましたね。では、6×5をしてみてください。
それでは計算をしてみましょう。「まず、D尺の6に、C尺の1をあわせます。そして、C尺の5にカーソル線を合わせれば…??」

お分かりいただけましたね。C尺の5にカーソル線をあわせることができないのです。こういった状態を目外れ(めはずれ)といいます。「計算尺って6×5なんて簡単な式ができないのか。」なんて落胆しないでくださいね。ちゃんとできます。こんなときは、はじめにD尺の6にC尺の1をあわせるのではなく、D尺の6にC尺の10をあわせるのです。
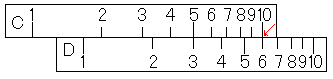
「そして、C尺の5にカーソル線を移せば…」。それでも、なんか変ですね。これでは、「6×5=3」になってしまいそうです。
しかし、これは問題ないのです。計算尺は数字の有効数字の部分(仮数部分)だけを計算する道具です。だから、計算尺にとっては3も30も0.3も、さらに3000も同じ場所に答えが出るのです。
では、どうやって3なのか30なのか0.3なのか、はたまた3000なのか決めるのでしょうか?それは、人がやるしかありません。「6×5が3や0.3や3000になることはないだろう」ということは勘で分かりますよね。
今までの計算では、メモリの値がそのまま答えになるものばかりでした。しかし、これはたまたま同じだっただけで、本来ならば、D尺の目盛りを読んだ後、位取りを考えなければならなかったのです。
まだ疑問は残ります。では、C尺の1をあわせるか、C尺の10をあわせるかはどうやって決めるのでしょうか?実はこれも勘に頼ります。仮にC尺の1をあわせたとして、メモリが読めなさそうだったらC尺の10を使います。
計算尺は、計算尺と人の共同作業で答えを出すのです。電卓の場合、ただボタンをたたくだけで答えが出ましたが、計算尺の場合頭も使います。計算していると数学の勉強も一緒に出来てしまいます。
それでは、今までのことを踏まえて、計算尺で計算してみてください。
それでは、C尺の1をあわせる場合と、C尺の10を合わせる場合を混ぜてみたいと思います。さらに位取りも考えてみてください。
だいぶ慣れてきましたか?思いついた数字を掛けてみてください。
C尺の10を用いたときの原理を紹介します。
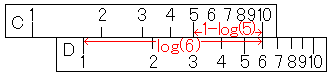
C尺の1からC尺の5までの長さがlog(5)になりますから、C尺の5からC尺の10までの長さは1-log(5)になります。すると、D尺の1とC尺の5との距離は次のようになります。
log(6) - {1 - log(5)}
= log(6) - 1 + log(5)
= log(6) + log(0.1) + log(5)
= log(6 × 0.1 × 5)
= log(3)
したがって、有効数字の部分の3が求まったのです。