このページでは、連続計算の仕方を紹介します。掛け算・割り算のまとめで紹介したことを前提として話を進めていきますので、まだお読みになっていない方は、こちらをご覧下さい。
掛け算の連続計算をご覧の方は、何も説明しなくてもお分かりのことと思います。ここでは、簡単にC尺とD尺を使った計算のやり方を述べるだけにします。
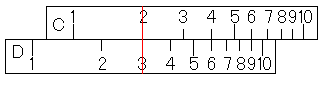
「30÷2÷3」の計算です。
1.~3.が「30÷2」の計算です。実際、3.で、C尺の1に対応するメモリを読むと「30÷2=15」ですよね。位取りは自分で考えるのでした。3.~5.が「(30÷2の答え)÷3」の計算です。
掛け算の連続計算のときと同様、3.で、「30÷2」の答えを読む必要はありません。上での計算例でも、メモリを読んでいませんよね。
上で紹介した方法を使えば、どんな割り算でもできます。しかし、何度も滑尺やカーソルを動かさなければならず、長い計算では大変不便です。そこで、ちょっと楽できる計算方法を紹介します。
それは、C尺とD尺だけではなく、CI尺も使う方法です。今までのページで、C尺を使った割り算と、CI尺を使った割り算の2種類紹介しました。「どうして同じ割り算をするのに2種類もあるのか?」と疑問に思った方がいらっしゃるかもしれません。それは、連続計算で使うためだったのです。掛け算の連続計算のときでもそうでしたよね。
では、具体的に計算をしてみましょう。ここでは先ほどと同じ30÷2÷3をしてみたいと思います。ここでも、先に30÷2をするのは同じです。
まず、30÷2です。では、やってみましょう。D尺の3にカーソル線を合わせます。そして、カーソル線にC尺の2を合わせます。

カーソルを動かして、C尺の1に合わせます。
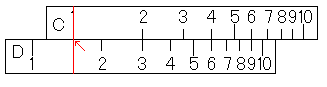
すると、矢印の位置に30÷2の答えを感じますよね。しかし、この値を読まなくてもいいです。だからわざとメモリを振っていません。
今、私たちは「30÷2÷3」のうち、「30÷2」までやりました。後は、この値を3で割るだけです。
ここで、先ほどはC尺を使いましたが、今度はCI尺を使って計算したいのです。CI尺を使った計算の方法を覚えていますか?
このうち、「D尺の割られる数にCI尺の1を合わせる」というのはすでにできています。なので、カーソル線をCI尺の3に合わせるところから続けます。
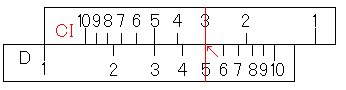
そうすると、D尺に5が求まっています。
ここで注意してほしいのが、「一度カーソル線をC尺の1に合わせたが、そのまますぐにCI尺の3に移動した」ということです。つまりカーソル線をC尺の1に合わせた動作は無駄だったのです。効率よく計算するには、この作業を省かなくてはなりません。カーソル線をC尺の1に合わせることなく計算する練習をしてみてください。
以上、割り算の連続計算の方法を2種類紹介しました。どちらが簡単だったでしょうか?2.はカーソル線をC尺の1に合わせることなく計算したときで比較します。手順は2.のほうが複雑なので、2.は面倒くさいと思ったかもしれません。しかし、計算の手続きとしては2.の方が少ないのです。今のところは3つの数の割り算までしか紹介していませんが、次の項目で紹介する4個、5個の数字の割り算になるとその差は顕著になります。2.の方法での連続計算の計算方法を練習してみてください。
1個ずつ計算していく、1.の方法はお分かりいただけると思いますので、C尺とCI尺の両方を用いた2.の計算方法を紹介します。
例によって簡単な式で説明します。前の計算式にちょっとだけ数を足してみました。「30÷2÷3÷2」です。30÷2÷3の部分は2.で紹介した方法で計算しますので省略します。

D尺に5が求まっています。
ここまでは、前の例の通り計算すればできます。
ここからが新しいことです。今の計算尺の状態をじっと眺めてください。私たちはあと、1つの数字で割らなければなりません。その割る対象(5)はD尺にいます。また、カーソル線はその数字(5)に合っています。
この後、どうやって2で割りましょうか?割り算の方法は2種類知っています。そのうちどちらが楽でしょうか?この場合、C尺を使う方法はC尺の2をカーソル線にあわせるだけでOKです。それに対して、CI尺を使う方法ではCI尺の1をカーソル線に合わせ、その後、カーソルを移動しなければなりません。それならば、C尺を使ったほうが楽ですよね。ということで、C尺の2をカーソル線に合わせます。
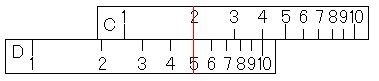
そして、C尺の1の下のD尺のメモリを読めば「30÷2÷3÷2=2.5」が求まったのです。
今まで、いくつかC尺とCI尺を使った連続計算をしてきましたが、ある程度ポイントをつかむことができていると思います。私たちが第一に考えることは、「楽をすること」。このあと、C尺を使ったほうが楽か、それともCI尺を使ったほうが楽なのか、それを考えれば、一番楽な方法で計算を進めることができます。
幸い、連続計算には一定のルールがあります。それは「逆・逆・逆…」です。つまり、「C尺を使ったら今度はCI尺、その次はC尺、そのまた次はCI尺、そのまたまた先はC尺…」ということです。そうすると、無駄なく計算することができます。これは掛け算のときにも同じでしたよね。
上の例では「30÷2÷3÷2」の「30÷2」の計算をC尺を使いましたが、CI尺を使って計算を始めても構いません。ただ、割り算はC尺を使ったほうが楽ですから、C尺からはじめることが多いようです。
これは、次の次で説明する、掛け算と割り算が混ざった連続計算のときにとても役立つのですが、次のようなルールがあります。
それから、C尺を使って割り算をした後、CI尺を使って連続計算をする場合ですが、このとき一度カーソルをC尺の1(あるいはC尺の10)にあわせていると、それは無駄な動作です。なぜなら、カーソル線をC尺の1(あるいはC尺の10)にあわせた後、すぐにカーソルをCI尺の別のメモリに移動させるからです。そのときは、C尺を使って掛け算をした後、C尺の1(あるいはC尺の10)の下にその答えを感じながら、カーソル線を直接次のCI尺のメモリに動かし、計算を続けてください。