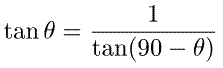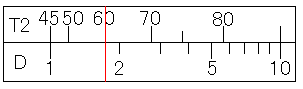
ここでは、tan(60度)を求めてみたいと思います。
T尺が2本ある計算尺では、一本が6度~45度、もう一本が45度~84度までの目盛が振られています。ここでは前者をT1尺、後者をT2尺と書きます。
このタイプの計算尺ではT2尺を利用することで簡単に求めることができます。T2尺の基線とD尺の基線を合わせて、T2尺の60度にカーソル線を合わせると、D尺に答えの1.732が求まります。
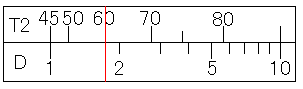
TI尺が2本ある計算尺では、一本が45度~6度、もう一本が84度~6度までの目盛が振られています。ここでは前者をTI1尺、後者をTI2尺と書きます。
このタイプの計算尺ではTI2尺を利用することで簡単に求めることができます。TI2尺の基線とDI尺の基線を合わせて、TI2尺の60度にカーソル線を合わせると、DI尺に答えの1.732が求まります。
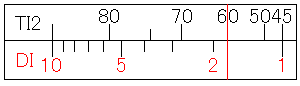
T尺が1本しかない場合、直接tan(60度)を示す尺や目盛はありませんが、簡単に計算することができます。それは、tanに関する次の公式を利用します。
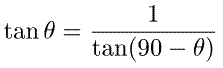
この公式を利用すれば、次のようになります。
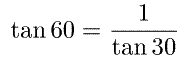
T1尺の30にカーソル線を合わせてください。そのままD尺を読むとtan(30度)なので、その逆数を求めるためにDI尺を読むと、答えの1.732を求めることができます。
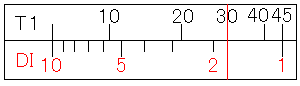
TI1尺の30にカーソル線を合わせてください。そのままDI尺を読むとtan(30度)なので、その逆数を求めるためにD尺を読むと、答えの1.732を求めることができます。
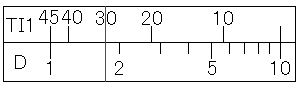
この場合は、やはり次の公式を用いて計算すれば、小さい角度のtanを求めることと、逆数を求めることに還元できます。小さい角度を求めることは、三角関数の値(2)で紹介しています。