高校の数学で、「正弦定理」「余弦定理」というものを習います。ここでは簡単に正弦定理と余弦定理についてまとめてみましょう。
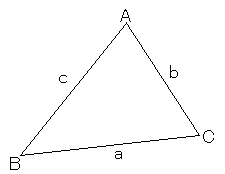
下の図のような三角形ABCについて考えます。

このとき、次の関係式が成立します。
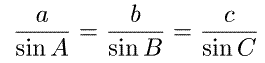
これを正弦定理といいます。
また、次のような関係式も成立します。
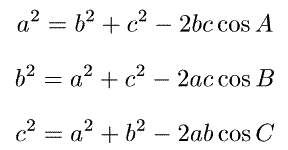
これを余弦定理といいます。
正弦定理は、上で紹介したとおり、長さと角度の三角関数の関係式を表しています。これらの関係は掛け算、割り算によって結び付けられているので、計算尺で簡単に計算することができます。
同じように余弦定理も長さと角度の関係式を表していますが、足し算や引き算によって結び付けられています。計算尺では足し算や引き算はできませんから、計算尺で余弦定理を利用することはできないのです。
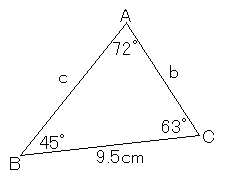
それでは、次の三角形の角度C, 長さb, cを求めてください。
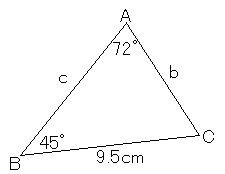
まず、角度Cは簡単に求めることができます。三角形の内角の和は180度ですから、
![]()
となります。
次に、正弦定理より、
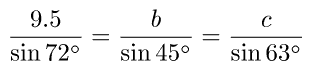
が成り立ちますので、
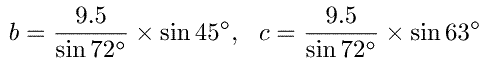
となります。あとはこれを計算尺で計算します。
D尺対応滑尺表型、つまり、三角関数尺がD尺に対応しており、両面計算尺で、滑尺に三角関数尺がある計算尺での計算が最も簡単ですので、これを利用します。
まず、D尺の9.5にS尺の72度を合わせます。
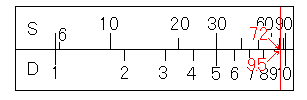
そして、S尺の45度にカーソル線を合わせ、D尺の目盛りを読むと、bの値7.06を読むことができます。
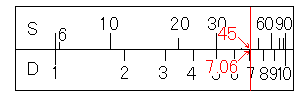
続けて、S尺の63度にカーソル線を合わせ、D尺の目盛りを読むと、cの値8.90を読むことができます。
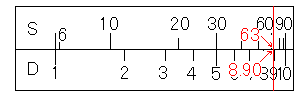
3.では、具体的な例で、計算式を出して答えを求めましたが、ここでは一般的にこの計算方法を見てみましょう。
もう一度、正弦定理を見てみます。
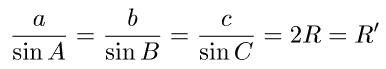
ここで、この式の値を2Rとおきました。このRには意味があり、三角形ABCの外接円の半径ですが、今回は利用しないので、これをR'とおきました。
上で紹介した例では、まず、「9.5 ÷sin 72度」の計算をしました。これはR'の値を求めたことになります。
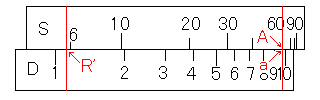
Bとb, Cとcからも、同じようにR'を求めることができます。
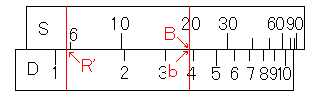
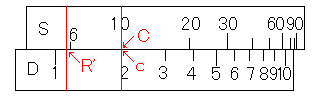
これを一枚の図にまとめてみましょう。
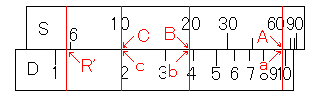
つまり、Aとa, Bとb, Cとcが対応するようになっているのです。上の例は長さを求めるものでしたが、この方法を利用すれば、角度を求めることもできます。