当委員会では、都合上計算尺を次のように分類しました。
このうち、D尺対応滑尺裏型は例外ですので、後に述べます。
その他の種類の計算尺で割り算をする時、それは普通の割り算と同様の方法で計算します。ただ、普通の割り算と違う点は、sin(何々)というときやtan(何々)というときは、S尺やT尺などを利用するということです。もう一つ、計算の順序を考えて、時には逆数を用いて計算しなくてはなりません。
抽象的過ぎるので、すこし具体的に説明しましょう。2÷3という計算をしたい時と、2÷sin(30)という計算をしたい時ではほとんど同様の操作をするということです。
C尺を利用する時は、D尺の2にカーソル線を合わせて、C尺の3をカーソル線に合わせましたよね。sin(30)で割りたいときは、C尺の3をカーソル線に合わせる代わりに、S尺の30を合わせるのです。違いはそれだけです。
tanの計算はsinの計算とまったく同じ方法です。sinの尺を用いる代わりに、tanの尺を使えばいいのです。そこで、sinの計算の方法のみを説明します。
では、具体的に計算尺の種類ごとに計算方法を見てみましょう。
D尺対応滑尺表型は、C尺とD尺で割り算をする時のように計算します。
ただし、A尺対応滑尺表型では、A尺とB尺で割り算をする時のように計算します。A尺対応滑尺表型では、「D尺」を「A尺」と読み替えてください。
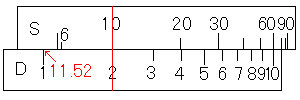
では、2÷sin(10)をしてみましょう。
まず、D尺の2にカーソル線を合わせます。次にカーソル線にS尺の10を合わせます。C尺の基線に対応するD尺の目盛りを読みます。

なんとなく読んでしまうと1.152になりそうですが、答えは11.52です。
sin(10)÷2のタイプは、まず2÷sin(10)を計算して、逆数を求めます。
このタイプは、CI尺とD尺で割り算をする時のように計算します。
では、2÷sin(10)をしてみましょう。
まず、D尺の2にSI尺の基線(つまりC尺の基線に同じ)を合わせます。次に、カーソル線をSIの10に合わせます。そして、カーソル線の下のD尺のメモリを読み取ります。
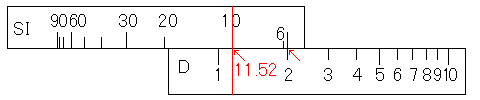
すると、答えの11.52が求まります。
sin(10)÷2のタイプは、まず2÷sin(10)を計算して、逆数を求めます。
このタイプは、まず、sinの値をD尺に移してから、計算します。
では、sin(10)÷2を計算してみましょう。
まず、S尺の10にカーソル線を合わせます。すると、D尺の目盛りはsin(10)となります。あとは、この値を2で割ることを考えます。そこで、C尺の2をカーソル線に合わせます。そして、C尺の基線に対応するD尺の目盛りを読み取ります。
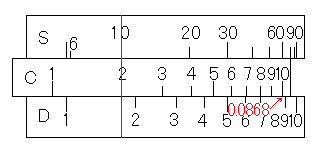
すると、答えの0.0868を読み取ることが出来ます。
2÷sin(10)のタイプは、まずsin(10)÷2を計算して、逆数を求めます。