さて、今までの単純な掛け算・割り算だけの計算からいよいよ脱出し、まずは、2乗・3乗・平方根・立方根の値を求めてみたいと思います。
「習うより慣れろ」と昔からいいますので、 まずは実際に2の2乗 (22)の値を求めてみたいと思います。
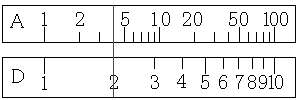
まず、今まで何度も使ってきたD尺の2にカーソルを合わせます。

そして、A尺の目盛りを読みます。
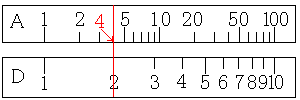
すると、答えの4を求めることができます。
今度は2の3乗 (23)を求めてみたいと思います。
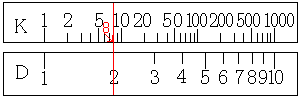
まず、先ほどと同様に、D尺の2にカーソル線を合わせます。
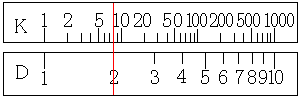
先ほどはA尺の目盛りを読みましたが、今度はK尺の目盛りを読みます。すると8が求まります。
では、4の平方根を求めましょう。
そもそも、平方根とは2乗の逆の計算なので、2乗と逆の操作をすれば平方根が求まりそうです。実際に計算をしてみます。
まず、A尺の4にカーソルを合わせます。

そして、D尺のメモリを読みます。すると、答えの2が求まります。
やはり、2乗を求めるときと全く逆の作業をすればOKです。
最後に、8の平方根を求めたいと思います。
先ほどと同様、やはり3乗を求める時と全く逆の作業をすればいいのです。
まず、K尺の8にカーソル線を合わせます。

そして、D尺の目盛りを読むと、答えの2が求まります。
A尺やK尺を使って2乗・3乗・平方根・立方根を求める時には、特に位取りに注意する必要があります。
A尺に振られているメモリは1から100です。つまり、1から10の2乗を求める時や1から100の平方根を求める時はメモリをそのまま読めばいいのです。
しかし、30の2乗を求める時は、3の2乗を求める時と同様、D尺の3を利用します。もともとの数(30と3)において位は1つしか違いませんが、答え(900と9)では位が2つ違ってきます。0.3の2乗を求める時も同様で、位が2つずれます。
K尺を用いる時でも注意が必要です。
K尺に振られているメモリは1から1000です。つまり、1から10の3乗を求める時や1から1000の立方根を求める時はメモリをそのまま読めばいいのです。
しかし、30の3乗を求める時は、3の3乗を求める時と同様、D尺の3を利用します。もともとの数(30と3)において位は1つしか違いませんが、答え(27000と27)では位が3つ違ってきます。0.3の3乗を求める時も同様で、位が3つずれます。
さらに注意が必要なのは、平方根・立方根を計算する時です。
平方根を求める時には、もとの数字を0.0001,0.01,1,100,10000で区切って計算するメモリを決定します。
上で述べたように、1から100の平方根を計算する時にはA尺の1からA尺の100を利用すればいいのですが、100から10000の平方根を計算する時にも、0.01から1の平方根を計算する時にもA尺の1からA尺の100を利用します。10から100の平方根を計算するのにA尺の1からA尺の10を利用したり、100から1000の平方根を求めるのにA尺の10からA尺の100を利用してはいけません。
具体的な例を表にまとめてみます。
| 求める値 | 利用する尺 |
|---|---|
| 0.0002の平方根を求める | A尺の 2 を用いる |
| 0.002の平方根を求める | A尺の20を用いる |
| 0.02の平方根を求める | A尺の 2 を用いる |
| 0.2の平方根を求める | A尺の20を用いる |
| 2の平方根を求める | A尺の 2 を用いる |
| 20の平方根を求める | A尺の20を用いる |
| 200の平方根を求める | A尺の 2 を用いる |
| 2000の平方根を求める | A尺の20を用いる |
| 20000の平方根を求める | A尺の 2 を用いる |
今度は立方根に関する表です。
| 求める値 | 利用する尺 |
|---|---|
| 0.0002の立方根を求める | K尺の200を用いる |
| 0.002の立方根を求める | K尺の 2 を用いる |
| 0.02の立方根を求める | K尺の 20 を用いる |
| 0.2の立方根を求める | K尺の200を用いる |
| 2の立方根を求める | K尺の 2 を用いる |
| 20の立方根を求める | K尺の 20 を用いる |
| 200の立方根を求める | K尺の200を用いる |
| 2000の立方根を求める | K尺の 2 を用いる |
| 20000の立方根を求める | K尺の 20 を用いる |
次の計算の原理でも述べるように、A尺やK尺は、D尺の半分あるいは3分の1の長さにしたものですから、読み取るとき、D尺で読むよりも誤差が大きくなります。
そこで、よりよい精度で計算するには、ふつ~に2乗・3乗を計算します。所詮、2乗は同じ数を2回、3乗は同じ数を3回掛け合わせたものですから、D尺・C尺・CI尺を使って掛け算をすれば、2乗・3乗の値が求まります。この場合、A尺やK尺を使って計算するよりも必ずよい精度で計算ができます。
ところが、平方根・立方根をかならずよりよい精度で計算する方法はありません。1に近い数の平方根や立方根を計算する時には後で述べるLL尺というのを利用するとかなり精度が上がりますが、10など、1からかなり外れた数の場合、反対に精度が落ちてしまいます。
少し数学の話が出てきますので、読み飛ばしてもかまいません。
では、じっくりD尺とA尺を見てみましょう。
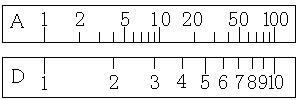
何となくお分かりいただけるでしょうか?D尺を半分の長さにして、2つつなぎ合わせたのがA尺です。それでは原理を簡単に紹介します。
D尺の1と、D尺のdとの間の距離は、log(d)になっているのでした。ここで、A尺について見てみると、A尺はD尺の長さを半分にして、2つつなぎ合わせたものです。つまり、A尺の1と、A尺のaとの間の距離は、log(a)/2になっています。この2つの長さが等しいとすると、log(d)=log(a)/2となります。これより、a=d2となることが分かります。つまり、A尺にはD尺の2乗が求まるのです。逆にd=√aとなりますので、D尺にはA尺の平方根が求まります。
今度は、D尺とK尺をじっくり見てみます。
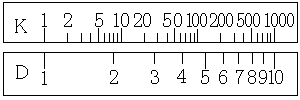
何となくお分かりいただけるでしょうか?D尺を3分の1の長さにして、3つつなぎ合わせたのがK尺です。それでは原理を簡単に紹介します。
D尺の1と、D尺のdとの間の距離は、log(d)になっているのでした。ここで、K尺について見てみると、K尺はD尺の長さを3分の1にして、3つつなぎ合わせたものです。つまり、K尺の1と、K尺のkとの間の距離は、log(k)/3になっています。この2つの長さが等しいとすると、log(d)=log(k)/3となります。これより、k=d3となることが分かります。つまり、K尺にはD尺の3乗が求まるのです。逆にd=3√kとなりますので、D尺にはK尺の立方根が求まります。