前のページで、2乗・3乗・平方根・立方根の値を求めることができるようになりました。このページでは、2乗・3乗を含んだ計算をしてみたいと思います。
このあたりから、計算の仕方を暗記するのは難しく(ややこしく)なってきます。ですので、実際に計算をする時には、原理を考えながら計算を進めていくようにします。その時のポイントもいっしょに書いておきますので、参考にしてください。このポイントを理解しておくと、2乗・3乗・平方根・立方根を含んだ計算をすらすら出来るようになります。
まず、2×32の計算をしてみます。
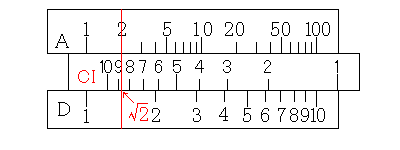
A尺の2にカーソル線を合わせてください。すると、D尺には√2が現れます。

次に、カーソル線にCI尺の3を合わせます。そして、カーソル線をCI尺の1に移動します。
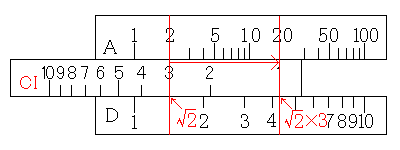
すると、カーソル線の下、D尺のメモリは、√2×3になります。したがって、A尺のメモリはD尺の2乗でしたから、(√2×3)2=2×32になります。
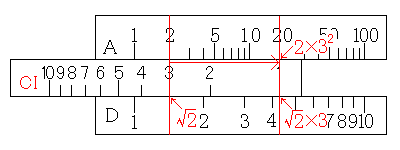
次は、32×2をやりたいのですが、これは計算の順番を変えれば2×32となります。つまり、上で計算した方法で計算することができます。
では、50÷52の計算をしてみましょう。すると、D尺のメモリは√50になります。
まず、A尺の50にカーソル線を合わせます。
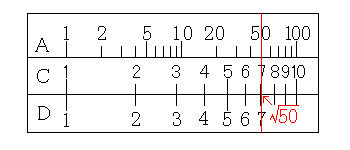
そこで、C尺の5をカーソル線に合わせます。
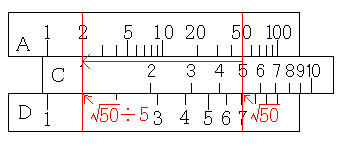
そして、カーソル線をC尺の1に合わせます。
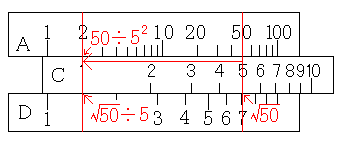
すると、D尺とC尺では√50÷5の計算をしたことになりますので、D尺のメモリは√50÷5になります。A尺はD尺の2乗になっているので、A尺のメモリは50÷52になっています。A尺の目盛りを読むと、答えは2です。
A尺を用いた計算方法を思いつきません。次で述べる方法で計算してください。
今まで、2乗を含んだ計算のしかたをみてきました。しかし、2乗は所詮同じ数字を2回かけただけのものです。ということは、A尺を使わなくても、次のように計算できるのです。
これらの計算は、C尺、CI尺、D尺を用いることで計算できます。
また、誤差のページで詳しく述べますが、A尺を用いると誤差が大きくなります。ではなぜA尺が存在するのかというと、平方根・立方根の計算はA尺を用いると計算が楽になるからです。
3乗を計算するにはK尺を用いるのですが、前のページで述べたように、K尺とA尺はほとんど同じ扱いで計算をすることができます。つまり、2×32の計算の場合、A尺を利用しましたが、2×33の場合、全く同様の計算をK尺を使ってすればよいのです。
3乗を含んだ計算の場合も、2乗を含んだ計算と同じように、K尺を利用しなくても、C尺、CI尺、D尺を利用することで計算することができます。