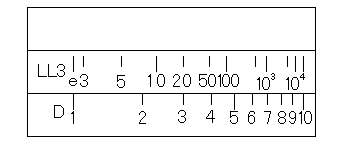
まずは、簡単にLL尺の復習をしてみましょう。LL尺というのは指数・対数の値で紹介したように、指数・対数の計算をするものです。
「LL尺」という尺が存在することはまれで、たいてい、LL3尺, LL2尺のように何本か準備されています。少ないもので主にこの2本、多いものでLL3, LL2, LL1, LL0, LL00, LL01, LL02, LL03尺の8本でしょう。また、LL00尺などは計算尺のメーカーや型番によってその呼び方がLL-0尺など様々です。
ここでは、これらすべてを総称してLL尺といい、個別の尺を指すときは、LL3尺などと明記します。
また、LL尺のある計算尺では、たいていのものがLL3尺とLL2尺を備えているので、この2本を例に話を進めていきたいと思います。
滑尺をひっくり返して滑尺の裏面を表面にすれば簡単に計算できますが、裏面を裏面として計算するのは大変です。私がただ単に計算方法を発見できなかっただけかもしれません。
まずは、ab、つまり、aのb乗を求めてみましょう。ここではその例として32を求めてみたいと思います。この例はD尺とA尺を利用すれば簡単に求めることができますが、ここではLL3尺を利用して求めます。
片面計算尺に限らず、計算尺は滑尺を固定尺から完全に取り出すことができます。そこで、滑尺を固定尺から完全に取り出して、裏面が表面になるように再度差し込んで、滑尺の裏面を表面にしてしまいましょう。

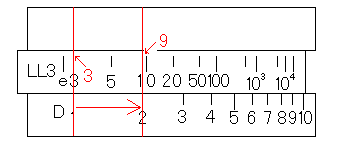
D尺の1にLL3尺の3を合わせます。そして、D尺の2にカーソル線をあわせ、カーソル線に対応するLL3尺の目盛りを読むと答えの9となります。
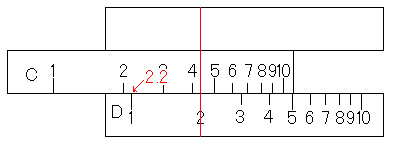
まず、裏面の基線にLL3尺の3を合わせます。
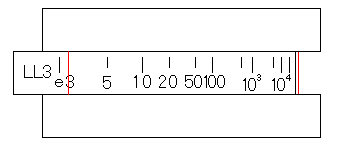
そして、そのまま表面を向け、D尺の2にカーソル線を合わせ、対応するC尺の目盛りを読みます。この例では2.2と読むことができます。
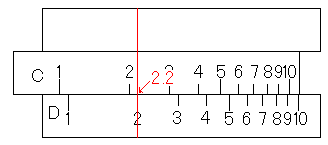
今度は、そのC尺の2.2をD尺の1に合わせます。
最後に、そのまま計算尺を裏返し、LL3尺の目盛りを読みます。すると、答えの9を読むことができます。
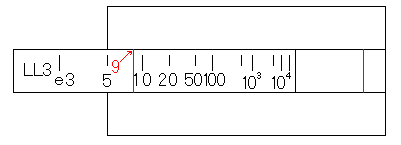
ab=cと置き、次のように式変形をすると、b=logacとなります。
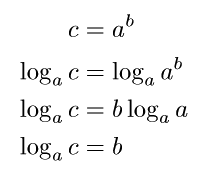
このことから、上で紹介したabの求め方を逆にたどっていけば、logacを求めることができます。そこで、実際にlog39を求めてみましょう。
まず、LL3尺の3をD尺の1に合わせます。そしてLL3尺の9にカーソル線をあわせ、D尺の目盛りを読むと答えの2を読むことができます。

まず、裏面の基線にLL3尺の9を合わせます。
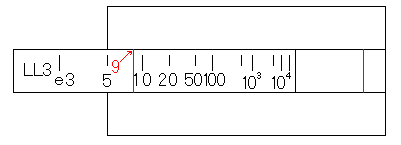
次に、表面にして、D尺の1に対応するC尺の目盛りを覚えておきます。ここでは2.2です。

再び裏面にして、LL3尺の3をカーソル線に合わせます。
最後に、計算尺を表面にして、カーソル線を、C尺の先ほど覚えておいた2.2に合わせます。

そしてD尺の目盛りを読めば、答えの2を読むことができます。