まずは、普通の定規の目盛りの読み方から見てみましょう。たとえば、10cmの定規であれば、次のようなものが一般的でしょう。
![]()
これは、数字が書いてあるところでは、左から順に「0cm, 1cm, 2cm, 3cm, 4cm, 5cm, 6cm, 7cm, 8cm, 9cm, 10cm」であることをあらわしています。
それでは、もう少し細かく見てみましょう。1と2のあいだを拡大してみたいと思います。

1と2のあいだにはメモリがあり、真ん中のものだけ長くなっています。真ん中のメモリを長くすることにより、この線が「何らかのきれいな数字」であることを表しています。今回の場合、それは1.5です。これはちょうど1と2の間の数字です。このような場合、「1.4が長くなっている」ということはありません。
そして、残りの数字は、その次に「何らかのきれいな数字」であることをあらわしています。このことをふまえると、これらのメモリは左から順に、「1.0cm, 1.1cm, 1.2cm, 1.3cm, 1.4cm, 1.5cm, 1.6cm, 1.7cm, 1.8cm, 1.9cm, 2.0cm」であることが分かります。
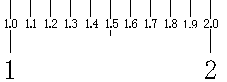
では、さらに拡大してみましょう。1.0と1.1のあいだを見てみます。

実際にメモリがあるわけではありませんが、1.0と1.1のあいだを目分量で10分の1まで分けることができます。つまり、メモリの10分の1まで読み取るということです。
以上のことを踏まえると、0.1cm刻みでメモリの振られた定規では、「0.00cm, 0.01cm, …, 9.99cm, 10.00cm」と読むことができます。
普通の定規の場合、メモリは等間隔に並んでいます。このような場合、メモリを読むことは簡単なことです。しかし、計算尺では、後述しますが、対数でメモリが振られています。そのため、たとえばC尺であれば、1~2の間隔と、2~3の間の間隔は違っています。
その上、1~2の間と、2~3の間では、メモリが振られている刻み幅※も違っています。実際にメモリを読むときには、メモリがどのように振られているかを判断して読むようにしなければなりません。
※このページでは、実際のメモリとメモリの間の距離ではなく、「いくつごとにメモリが振られているか」を意味するものとします。
それでは具体的に見て行きましょう。以下では一番普及していると思われる10インチの計算尺のうち一番基本の尺であるD尺を見てみましょう。
まず、D尺の全体を眺めてみましょう。D尺と言うのは、計算尺の固定尺の下側にあり、左端に「D」と表記のある尺です。D尺をみると、左から順に「1, 2, 3, 4, 5, 6, 7, 8, 9, 10」と書かれているのが分かるでしょう。計算尺によっては、「1.5」が書かれているものもありますし、「10」が「1」と表記されているものもあります。
![]()
メモリの間隔が次第に狭くなっていくのが分かるでしょう。また、1~2までは同じ刻み幅でメモリが刻まれていますが、2~5では、刻み幅が大きくなります。5~10になると、さらに刻み幅が大きくなります。このように、計算尺は、メモリは等間隔で並んでいません。また、尺の途中で、メモリの数字の刻み幅が変わることが多いのです。
次に、1~2の間を見てみましょう。
![]()
このメモリでは、両端の1.0, 2.0 のほかに、1.5 にも数字が書かれています。計算尺によっては1.5 の表記がないものや、何か別の記号によって記されているものもあります。
普通の定規と同じように、このメモリでも3種類の長さの目盛り線があります。そのなかで一番長いものは0.1ごとに書かれており、左から順番に「1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0」をあらわしています。
![]()
次に、二番目に長い線は0.05ごとに書かれています。一番長い線とあわせると、左から順に「1.00, 1.05, 1.10, 1.15, 1.20, 1.25, 1.30, 1.35, 1.40, 1.45, 1.50, 1.55, 1.60, 1.65, 1.70, 1.75, 1.80, 1.85, 1.90, 1.95, 2.00」となります。
さらに、一番短いメモリは0.01ごとに書かれています。一番長いメモリ線や二番目に長い目盛り線とあわせると、「1.00, 1.01, 1.02, 1.03, 1.04, 1.05, 1.06, 1.07, 1.08, 1.09, 1.10, 1.11, 1.12, …, 1.99, 2.00」となります。

以上が目盛り線から読み取れる範囲です。しかし、普通の定規でも0.01cmまで読み取ることができたように、計算尺でもメモリの10分の1まで読むことができます。たとえば、1.00と1.01の間を目分量で10等分して、「1.000, 1.001, 1.002, 1.003, 1.004, 1.005, 1.006, 1.007, 1.008, 1.009, 1.010」と読むことができます。
つまり、1~2の間では、4桁目まで読むことができます。
それでは、2~5を見てみましょう。10インチの計算尺の2~5は、大半は次のようになっています。ただし、この絵では横幅サイズの関係上2~4までです。
![]()
このように、一番長いメモリと、二番目に長いメモリで、「2.0, 2.0, …, 4.9, 5.0」という有効数字2桁の数字を表しています。
![]()
さらに、一番短いメモリは0.02間隔でかかれています。つまり、全てのメモリをあわせると、左から順番に「2.00, 2.02, 2.04, 2.06, 2.08, 2.10, 2.12, …, 4.98, 5.00」とメモリが振られていることになります。
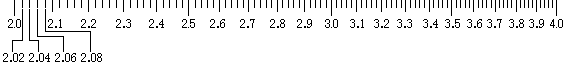
実際には、目分量でさらに細かく見ることがあります。一番多く用いられるのは、この最小のメモリ間隔0.02を半分まで見分けて、0.01単位で読み取る事です。つまり、1~2の範囲では0.001単位で、有効数字4桁で求めましたが、2~5の範囲では、有効数字3桁で「2.00, 2.01, 2.02, …, 4.99, 5.00」と読むことが多いです。また、判別は難しいのですが、2~3までの範囲は、0.001まで読み取って、有効数字4桁とすることもあります。
それでは、5~10の範囲を見てみましょう。
![]()
今回も、2~5の時と同様、一番長いメモリと、二番目に長いメモリで、「5.0, 5.1, 5.2, …, 9.9, 10.0」という有効数字2桁の数字を表しています。
![]()
2~5とは違って、一番小さいメモリは0.05間隔で刻まれています。図には書き込めませんので書きませんが、全てのメモリをあわせると左から順番に「5.00, 5.05, 5.10, 5.15, …, 9.95, 10.00」となります。
先ほどと同様に、実際には、目分量でさらに細かく見ることがあります。一番多く用いられるのは、この最小のメモリ間隔0.05をさらに目分量で5等分まで見分けて、0.01単位で読み取る事です。つまり、有効数字3桁で「5.00, 5.01, 5.02, …, 5.99, 10.00」と読むことが多いです。
それぞれの場合において、目分量でメモリの間隔以下を読み取ると言いました。そこで疑問が浮かぶのですが、例えば「メモリの半分」とは、本当にメモリとメモリの中点を見ればいいのでしょうか。よく計算尺のメモリを見ると、1と3の中点は2とはならず、約1.732となっています。「メモリの半分」というのは、メモリとメモリの中点を見るのではなく、中点より少し右側を見るべきではないのでしょうか?
結論から言うと、「メモリの半分」とは、メモリとメモリの中点を見れば良いということになります。これは簡単に言うとグラフに接線を引く作業とよく似ています。
グラフに接線を引く場合、大きい範囲で見ればグラフそのものと接線とは大きく離れていますが、接線の接点付近で見るとグラフと接線はほぼ同じに見えます。つまり、グラフは直線で近似できるということです。
計算尺のメモリも同じです。計算尺の尺全体で見れば目盛りは等間隔に並んでいませんが、ごく狭い範囲で見ると等間隔で並んでいるように見えます。具体的に1.0と1.1の間を良く見てください。ほとんど等間隔にメモリが並んでいますよね。このことから、「メモリとメモリの間」というごく狭い範囲では「メモリの半分」は「メモリとメモリの中点」と考えてよいのです。