皆さんは、比例と反比例をご存知ですね。ここで言う比例とは、正比例のことです。手元にある広辞苑には、次のように載っています。
正比例…二つの量xとyが相関連して変化し、その比が常に一定の値kである時、すなわちy=kxである時、両者は正比例するという。
反比例…一つの量が他の量の逆数に比例すること。逆比例。
つまり、反比例はy=k/xということですね。
計算尺で比例の計算をする前に、すこし、数学的な準備をしましょう。といっても、中学生程度の話です。いま、xとyが比例関係にあるとします。つまりy=kxです。そして、2つの数字の組、(x1,y1)、(x2,y2)がy1=kx1、y2=kx2を満たしているとしましょう。すると、k=y1/x1、k=y2/x2ですから、y1/x1=y2/x2が成立します。この式を変形すると、y2=y1/x1×x2となります。
2.1.より、y2=y1/x1×x2でした。では、実際に計算して見ましょう。いま、xとyが比例の関係にあり、それがx=3,y=2を満たしています。この時、x=9のときのyの値と、y=4のときのxの値を求めましょう。
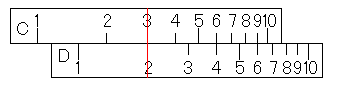
まず、x=9のときのyの値から求めてみましょう。y2=y1/x1×x2でしたから、2÷3×9をすればいいですね。まず、2÷3を計算します。ここではC尺とD尺を使って計算したいと思います。

今、C尺の10に対応するD尺に2÷3の答えがありますよね。この値に9を掛ければいいのです。どうすればいいでしょうか?連続計算を思い出してください。そうですね。カーソル線をC尺の9に持っていけばいいのでした。
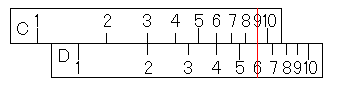
ここで、x=2のときのyの値を考えてみましょう。それも、カーソル線をC尺の2にあわせるだけで答えが出ますよね。
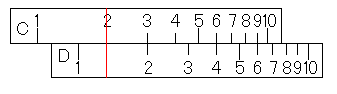
もうお気づきでしょうか?C尺をx、D尺をyと見れば、xとyの対応表になっているのです。
そうと分かってしまえば、y=4のときのxは簡単に求まりますよね。D尺がyでしたから、D尺の4にカーソル線を合わせればいいのです。
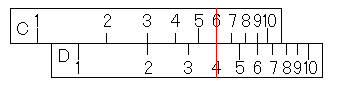
すると、めでたくx=6を得ることができました。
今回は具体的なxとyの点が分かっていたのでそれを使いましたが、「yがxの1.13倍」と分かって入れば、C尺の1をD尺の1.13にあわせればいいのです。すると、C尺がx、D尺がyの換算表になります。また、はじめの滑尺の合わせ方を変えれば(たとえば、上の例ではC尺の1.13にD尺の1にあわせれば)、C尺がy、D尺がxとなります。とにかく、最初にあわせた時、どちらがxで、どちらがyなのかをしっかり覚えていてください。
また、CF尺、DF尺、CIF尺はC尺、D尺、CI尺をずらしたものでした。なので、目外れが起きてメモリが読めない時、CF尺、DF尺、CIF尺をC尺、D尺、CI尺だと思って使うことができます。
キロメートルとマイルの換算をしてみましょう。手元にある理科年表を見ると、「マイル=1.6093km」となっています。計算尺で1.6093を表現するのは大変なので、今回は1.609のメモリをあわせたいと思います。では、C尺の1をD尺の1.609にあわせて下さい。「1.609なんていう線がない」と思われるかもしれませんが、10インチ(25cm)計算尺の場合、1.60と1.61のメモリがありますよね。それを見ながら1.609にあわせて下さい。5インチ(12.5cm)の場合は1.60と1.62のメモリがあります。大体その中央にあわせれば1.609になりますね。
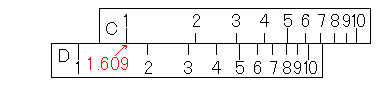
これでC尺がマイル、D尺がキロメートルの換算表ができました。2キロメートルが何マイルかはD尺の2にカーソル線を合わせれば分かりますよね。同じように、2マイルが何キロメートルかはC尺の2にカーソル線を合わせれば分かります。
計算尺で比例の計算をする前に、すこし、数学的な準備をしましょう。といっても、やはり中学生程度の話です。いま、xとyが反比例関係にあるとします。つまりy=k/xです。そして、2つの数字の組、(x1,y1)、(x2,y2)がy1=k/x1、y2=k/x2を満たしているとしましょう。すると、k=y1x1、k=y2x2ですから、y1x1=y2x2が成立します。この式を変形すると、y2=y1x1÷x2となります。
3.1.より、y2=y1x1÷x2でした。では、実際に計算して見ましょう。いま、xとyが反比例の関係にあり、それがx=3,y=2を満たしています。この時、x=5のときのyの値と、y=4のときのxの値を求めましょう。
まず、x=5のときのyの値から求めてみましょう。y2=y1x1÷x2でしたから、2×3÷5をすればいいですね。まず、2×3を計算します。ここではCI尺とD尺を使って計算したいと思います。
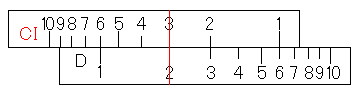
今、掛け算の答えはCI尺の1に対応するD尺のところにありますよね。あとはこの値を5で割ればいいのです。連続計算を思い出せば、CI尺の5にカーソル線を合わせればいいとわかりますよね。
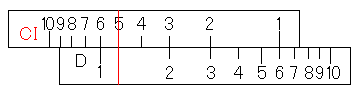
さて、先ほどと同じ展開ですが、CI尺とD尺がxとyの対応表になっていると分かります。しかも今回はさっきよりも特殊ですね。先ほどはxとyの区別がありました。つまり、たとえば、C尺がx、D尺がyだと覚えていなければなりませんでした。しかし反比例の時はどちらがどちらでも問題ありません。CI尺とD尺を区別する必要がないのです。それはy2=y1x1÷x2であり、x2=y1x1÷y2であることから分かります。
また、CF尺、DF尺、CIF尺はC尺、D尺、CI尺をずらしたものでした。なので、目外れが起きてメモリが読めない時、CF尺、DF尺、CIF尺をC尺、D尺、CI尺だと思って使うことができます。
3キロメートルの道のりを歩くことを考えます。その時、歩く早さと、かかる時間は反比例になります。時速3キロメートルで歩いた時は1時間かかりますから、D尺の3とC尺の1とを合わせます。
まず、時速6キロで歩いたら、何時間かかるでしょうか?カーソル線をD尺の6に合わせればCI尺に5を読み取れますね。CI尺の6にあわせてD尺の5を読み取っても構いません。答えは5時間ですか?違いますね。0.5時間です。30分です。あわてて5時間だとか、50分だとかと読み誤らないように注意してください。
では、2時間で着くためには時速何キロメートルで歩けばいいでしょうか?困りましたね。CI尺の2にも、D尺の2にもカーソル線をあわせることができません。こんな時に役立つのがCF尺、DF尺、CIF尺です。CF尺、DF尺、CIF尺はC尺、D尺、CI尺をずらしたものでした。なので、目外れが起きてメモリが読めない時、CF尺、DF尺、CIF尺をC尺、D尺、CI尺だと思って使うことができます。実際に、DF尺の2にカーソル線を合わせてください。CIF尺に1.5を読むことができます。あるいはCIF尺の2にカーソル線を合わせてください。DF尺に1.5を読むことができます。CF尺、DF尺、CIF尺は慣れてしまえば大変便利なものです。