
それでは、実際に割り算をしてみましょう。
まだ、計算尺をお持ちでない方は、ここをご覧下さい。
では、初めての割り算は、「8÷4」をしてみたいと思います。
まず、D尺の8にカーソル線を合わせます。下の図は、C尺とD尺がずれていますが、これは、「このとき、C尺とD尺がずれていても問題ない」ということを示しています。

次に、カーソル線と、固定尺をずらさないように注意しながら、滑尺を滑らせて、カーソル線にC尺の4を合わせます。
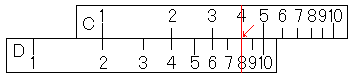
そして、C尺の1のすぐ下のD尺のメモリを読むと、2になっています。つまり、「8÷4=2」です。
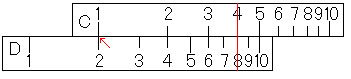
では、「6÷2」をやってみてください。上の説明を見ながらで結構です。当然「3」になりましたよね。
それでは、少しだけ数式を出しますので、計算尺で計算してみてください。
計算尺は値を近似値で出します。なので正確な値を求めることはできません。しかし、正確な値にたいした意味がないことは以前説明しました。それから、位取りは自分で考えなければなりませんでした。
例によって、「計算の原理なんか分からなくてもいい」という方や、「数学嫌い」という人は、この項目を読み飛ばしてもかまいません。読みたくなったら読んでください。
さて、割り算の原理ですが、これは掛け算の原理を知っていれば、簡単に分かりますよね。割り算は、掛け算の逆の計算です。だから、割り算の仕方は、掛け算の仕方の逆になっています。
では、上で紹介した「8÷4=2」について考えてみましょう。
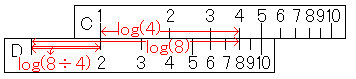
この図でお分かりいただけるでしょうか。log(x÷y)=log(x)-log(y)という関係式がありましたよね。つまり、D尺で長さlog(8)、C尺で長さlog(4)を準備しておけば、D尺の1からD尺の2の位置までの長さはlog(8)-log(4)=log(8÷4)になっているのです。
これで割り算ができるようになりましたね。では、3÷6をしてみてください。
「まず、D尺の3にカーソルを合わせます。次にC尺の6をカーソル線に合わせる。そして、C尺の1を見てみれば…??」
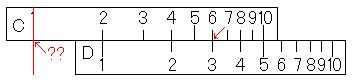
前のページと同じ構成なのでばればれですね。C尺の1の下にはメモリがありません。前回と同様、計算尺では3÷6ができないというわけではありません。こんなときは、最後にC尺の1を見るのではなく、、C尺の10の下を見ればいいのです。
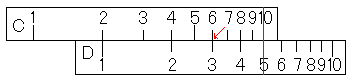
計算尺は、桁数は関係なく、有効数字の部分の計算のみをするということを考えると、これで「3÷6=0.5」ができていると分かりますね。
それでは計算してみましょう。やはり、C尺の1を見るか、C尺の10を見るかは、それぞれ考えてみてくださいね。メモリが存在するほうを見ればいいのです。