
多くの計算尺の上のほうに、CF尺、DF尺、CIF尺というのがあると思います。CIF尺だけがないものもあります。若干の例外もありますが、たいていπやルート10から始まっています。しかし、そのことを除けば、それぞれC尺、D尺、CI尺にとても似ています。ただ、少しずつずれているだけという印象を受けます。
実際、上で述べた事柄は正解です。CF尺、DF尺、CIF尺は、C尺、D尺、CI尺をずらして配置したものです。どれくらいずらしているかというと、πやルート10分だけです。
では、CF尺、DF尺、CIF尺は何のために使うのでしょうか?それは、計算尺の欠点を改善するために使われます。
その欠点というのは、目外れです。皆さんは計算していてメモリが読めなくて困ったことはありませんか?そんなとき、CF尺、DF尺、CIF尺を使うと、うまく読めることがあります。しかし、これは完全ではありません。読めないときもあります。ですが、読めるときが格段に増えます。
まだ、CF尺、DF尺、CIF尺を使う利点があります。それは、1に近い値のメモリを計算尺の中央付近で読むことができるということです。実際にはC尺、D尺、CI尺で読める場合でも、中央で目盛りを読んだほうが効率がよくなります。
さらに、1付近の計算が楽になるという点もあります。たとえば、「9×8×7×6」をやってみてください。C尺、D尺、CI尺で計算をしようと思うと結構大変だと思います。しかし、CF尺、DF尺、CIF尺を使うと、比較的楽に計算できます。
CF尺、DF尺、CIF尺単独の計算は、CF尺、DF尺、CIF尺がそれぞれC尺、D尺、CI尺だと思って計算します。計算方法は、C尺、D尺、CI尺での計算のときとまったく同じです。具体例として、DF尺とCIF尺を使った掛け算の方法を紹介します。
「6×2」の仕方です。
まったく同じ方法ですよね。同様に、C尺を使った掛け算と同じ方法で、CF尺を使った掛け算ができます。C尺を使った割り算と同じ方法でCF尺を使った割り算ができます。CI尺を使った割り算と同じ方法でCIF尺を使った割り算ができます。連続計算も同様です。
CF尺、DF尺、CIF尺を使う長所は上に述べた通りです。では、「9×8×7×6」をやってみてください。慣れるまでは大変ですが、慣れてしまうと重宝します。
これは、一見複雑に思えますが、実は使用頻度が高いものです。目外れを完全になくすことはできませんが、ある程度は解消できます。
では、具体的な計算方法ですが、これは覚えることはありません。ひとつ、イメージをしっかり焼き付けてほしいだけです。それは、「CF尺、DF尺、CIF尺はC尺、D尺、CI尺を少しずつずらしたものである」ということです。
何の事だかさっぱり分かりませんね。では、「3.2×3.2」をC尺を使って計算することを考えます。この場合、位の見積もりが大変ですね。一見、一の位までか、十の位まであるのかが分かりません。ということは、C尺の1を使うか、10を使うかの見当をつけるのが難しいということです。
それでは、C尺の1をD尺の3.2にあわせて下さい。そして、カーソル線をC尺の3.2に合わせることができれば成功です…。どうですか?ギリギリのところではみ出ていますよね。まれに10を越えた先までメモリが振ってある計算尺もありますが、たいていのものは目外れで目盛りを読むことはできません。

そんなときに役立つのがCF尺、DF尺、CIF尺です。ここでは、CF尺で説明しますが、ほかのものも同様です。CF尺はC尺をずらしたものでした。
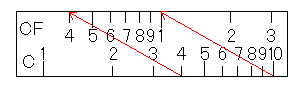
計算尺では、位取りは関係ないのでしたから、次のように見ることもできます。
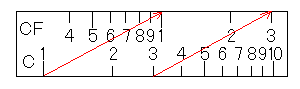
さて、今回の計算ですが、C尺の3.2にカーソル線をあわせることができないのでした。しかし、CF尺はC尺をずらして配置したものです。では、CF尺の3.2にカーソル線を合わせてみてください。
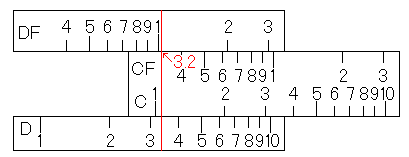
上の図では分かりにくいかもしれませんが、CF尺の3.2にカーソル線をあわせることができると思います。そして、D尺の変わりに、DF尺のメモリを読んでください。答えの10.24が読み取れると思います。
ちょっと分かりにくかったでしょうか?先ほども書きましたが、CF尺、DF尺、CIF尺をうまく使うためには、CF尺、DF尺、CIF尺はC尺、D尺、CI尺をずらしたものだというイメージをしっかり焼き付けるのがいいと思います。「C尺の3.2に合わせたかったけど、合わせられない。CF尺は、C尺を平行移動したものだから、C尺の変わりにCF尺の3.2を使おう!本来ならD尺で答えを読むけど、さっきCF尺を使ったから、今回はD尺ではなくDF尺を使おう!なぜならCF尺と同じように、DF尺はD尺をずらしたものだから。」こんな感じに覚えてください。やっているうちに、CF尺、DF尺、CIF尺の使い方が分かってくると思います。
では、ここで10の階乗(10! , 10×9×8×7×6×5×4×3×2×1)を計算してみてください。ただし、ここは計算尺のページですので、計算尺を使って有効数字2桁で求めます。それから、大きい数字から掛けてください。小さいほうから書けると、6の階乗が720となり、その時まで目盛りの線と一致してしまいます。実際に計算尺で求めたいときは、小さい数字から掛けた方がいいのですが、それでは練習になりません。必ず、大きい数字から掛けてください。
少しだけ、ポイントを述べます。まず、10と1は掛けないということです。10を掛けても所詮位取りが変わるだけ、1を掛けたところで何も変わりません。だから、10×9×8×7×6×5×4×3×2×1をするとはいえ、実際に計算するのは9×8×7×6×5×4×3×2です。
C尺とD尺、あるいはCI尺とD尺を使って計算しようとすると面倒なことになります。今回の一番初めの計算はDF尺とCIF尺を使って計算すると効率が良くなります。それは、計算尺の中央付近で計算できるからです。
まず、DF尺の9にカーソル線を合わせます。そしてカーソル線にCIF尺の8を合わせます。カーソルを動かしてCF尺の7に合わせます。滑尺を滑らせて、CIF尺の6を合わせます。そしてその次に、CF尺の5にカーソル線を合わせたいところですが、困ったことがおきます。今度はCF尺の5にカーソル線を合わせられないのです。そのときは、CF尺の5にカーソルを合わせる代わりに、C尺の5にカーソル線を合わせてください。これで計算がCF尺、DF尺、CIF尺を使ったものからC尺、D尺、CI尺を使ったものに移ったのですから、これから先はC尺、D尺、CI尺を使って計算します。CI尺の4をカーソルにあわせて…と計算していくと、答えが出ます。
答えは3628800です。有効数字が2桁ですから、3.6×106になります。最後に位取りを合わせますが、10を掛けるのを忘れないで下さい。