双曲線関数の値(2)

１．LL尺を用いて

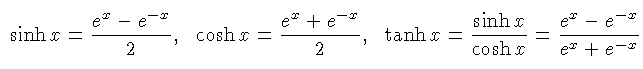
前のページの双曲線関数の定義をもう一度見てみましょう。

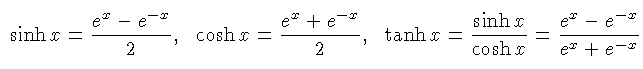
tanh(x)の値はsinh(x)とcosh(x)の値を求めれば割り算で計算できますので、sinh(x)とcosh(x)を求めることを考えてみます。

sinh(x)もcosh(x)もe^xとe^-xの値を求めれば求めることができます。これはLL尺を用いて計算することができます。

２．sinh(1.5)とcosh(1.5)、tanh(1.5)の計算

それでは、sinh(1.5)とcosh(1.5)を求めてみましょう。そのためにはまずe^1.5とe^-1.5を求めます。

D尺の1.5にカーソル線をあわせます。

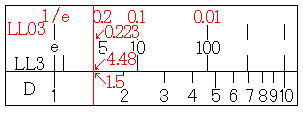
すると、LL3尺にe^1.5=4.48、LL03尺にe^-1.5=0.223が求まります。LL3尺からは小数第2位までしか求まっていませんから、LL03尺をe^-1.5=0.22と読みます。

coshの定義から、これを足して2で割ればcosh(1.5)=(4.48+0.22)÷2=2.35が求まります。実際にcosh(1.5)=2.35240961524325です。

また、sinhの定義から、sinh(1.5)=(4.48-0.22)÷2=2.13が求まります。実際にsinh(1.5)=2.12927945509482です。

tanh(1.5)を計算すると、sinh(1.5)÷cosh(1.5)=0.906となります。実際tanh(1.5)=0.905148253644866です。

３．sinh(0.2)とcosh(0.2)、tanh(0.2)の計算

次に、sinh(0.2)とcosh(0.2)、tanh(0.2)を求めてみましょう。前回と同様、e^0.2とe^-0.2を求めます。

LL尺の使い方を思い出してみましょう。今回はD尺の2にカーソルを合わせて、LL2尺、LL02尺の目盛りを読み取ります。

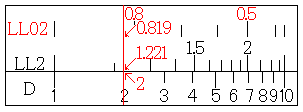
すると、LL2尺にe^0.2=1.221、LL02尺にe^-0.2=0.819が求まります。

coshの定義から、これを足して2で割ればcosh(0.2)=(1.221+0.819)÷2=1.020が求まります。実際にcosh(0.2)=1.02006675561908です。

また、sinhの定義から、sinh(0.2)=(1.221-0.819)÷2=0.201が求まります。実際にsinh(0.2)=0.201336002541094です。

tanh(0.2)を計算すると、sinh(0.2)÷cosh(0.2)=0.197となります。実際tanh(0.2)=0.197375320224904です。